Neuroscience with particle physics level confidence
PART 1. Our tools are imperfect. When I first got into neuroscience, I started deep down into neural circuitry: individual neurons and synapses. It was exciting to get glimpses into the nuts and bolts of what makes neural circuitry support the amazing behaviors we see in animals. I love patch clamp electrophysiology in all of its forms. The data itself is viscerally satisfying on multiple levels. It is all but perfect.

But most of the neuronal activity data we take in neuroscience has lower fidelity. Many of our tools are quite primitive. A great deal of what we learn about population level activity is from shoving metal electrodes into brains, which we’ve done for 100 years. Sure, we make them smaller now, and I’m a big supporter of Neuropixels and similar efforts, but the approach is still fundamentally crude.
Calcium imaging is more technically interesting– especially multiphoton calcium imaging. One problem with calcium imaging is: it’s not spikes. It’s a correlate of spiking, and that correlate’s usefulness can vary by cell type, reporter, and imaging parameters. Also, the time resolution is typically quite poor. So how can we hope to make meaningful measurements with calcium imaging? We want the measurements we report to be precise and accurate, so that they can be informative and support detailed analysis. Is it possible to do so with imperfect tools?
It is. All tools are imperfect. Still, with technical care and rigor, it is possible to obtain high fidelity results with some imperfect tools. After all, this is what experimental science– when it’s at its best– is all about. Experimental scientists make an art out of pulling exquisite measurements out of imperfect instruments. For example, particle physicists clumsily throw streams of particles at each other and make measurements of the trajectories of the products of the collisions. The idea is fundamentally a bit sloppy– definitely stochastic. Yet, by applying rigorous analysis, they can achieve exquisitely precise measurements, up to the level of five sigma.
I’m fortunate to get to work with a fellow scientist who places a premium on rigor: Dr. Yiyi Yu. This post is about a small portion of her recent work, and how she is making precise, accurate, and informative measurements of neural circuitry in action, despite the shortcomings of calcium imaging. Yiyi has been studying activity correlations in neural circuitry using calcium imaging, finding ways to make rigorous measurements, and using the results to obtain insights into principles of neural circuit function.
PART 2. Why measure activity correlations with calcium imaging? Activity correlations among neurons give us clues into how they are connected, how they might represent information, and how they might process it.
Who would bother to measure correlations with calcium imaging data? Isn’t the time resolution hopelessly poor? Isn’t the fidelity low? What’s wrong with you?
We weren’t the first to measure activity correlations with calcium imaging. In fact, there has been some nice work on the analysis of them. What is new in Yiyi’s study is two-fold: First, she used new instrumentation– large field-of-view two-photon imaging— to obtain one of the most extensive data sets in the field. Second, she subjected the data to several types of rigorous analysis that have not been previously explored. She obtained several fascinating insights, including (i) a new granular functional classification of visual cortical neuron tuning, (ii) evidence and an explanation of how correlations can actually increase at the millimeter length scale (rather than falling off with distance as they usually do), and (iii) evidence showing that noise correlations are more stable across stimulus types than signal correlations– that is, it appears as though noise correlations are a more stable measure of connectivity . If you want to learn more about those insights, please check out the preprint. What I want to focus on in the blog post is the rigor of analysis of correlations.
Yiyi systematically assessed the potential issues with noise correlations, and her work merits a highlight here.
Isn’t the time resolution of calcium imaging too low? No, it’s actually fine. Even in electrophysiology experiments where the raw data is sampled at > 10 kHz, spikes are often binned into bins that are 0.1 – 1.0 seconds wide, and this can help make more accurate measurements of correlated variability. This time resolution is well within the resolution of calcium imaging.
Isn’t the spike inference from calcium imaging uncertain? You miss individual spikes and can’t count the number of spikes in bursts. Right? True, and this is one of the most annoying things to me about calcium imaging. However, it doesn’t end up mattering as much as I thought it would. Yiyi did a very thorough analysis of this. Using electrophysiological recordings– thus we know the ground truth– she dropped individual spikes or spikes in bursts, and the estimated correlation values were mostly stable. That is, it takes a LOT of missing spikes to throw off these measurements. As long as you have enough data, correlation measurements are relatively robust to imprecise spike inference.
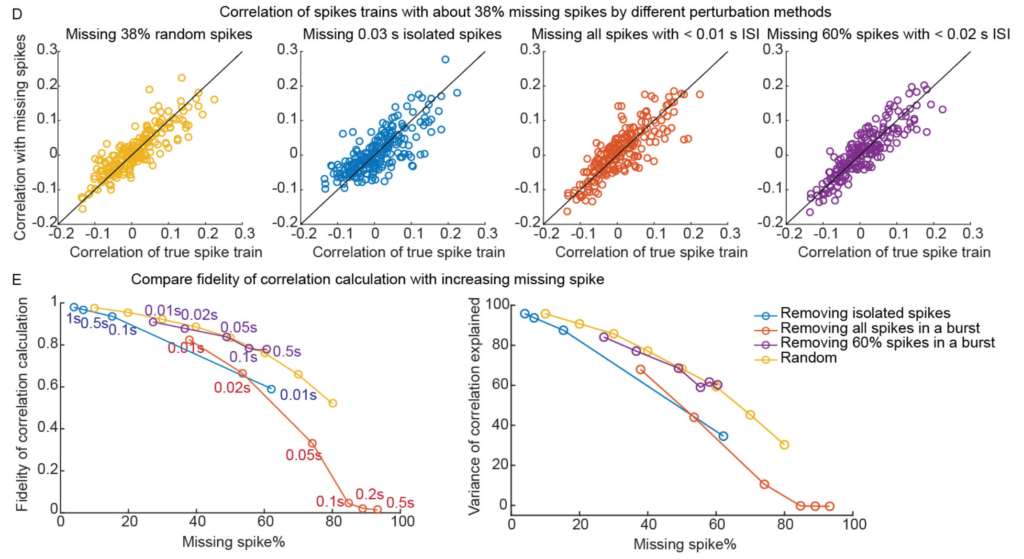
Don’t you need an unobtainable amount of data to get good measurements? Nope. You don’t. It is entirely feasible, given good instrumentation and experimental design, to get enough data to make precise measurements of noise correlations. Especially at the population level. Yiyi obtained measurements that have particle physics levels of confidence. Just 100 neuron pairs gets the error level below 0.01. This is particle physics-level precision, in a neuroscience experiment with imperfect tools.
Here is the preprint. There’s a lot in it. The measurements themselves, which this post discusses, and then the insights and modeling to help understand what the measurements can tell us. Excellent work by Yiyi.

Thanks for the interesting write-up! I had not noticed the preprint by Yiyi before, but did check it out after reading this blog post. And very interesting to read that missing a significant fraction of spikes does not pose a big problem for the correlation analysis.
When thinking about the title of this blog post, I’m wondering: do we really achieve “particle physics confidence levels” with this approach? If we are looking at neuron pairs, we use many neuron pairs from the same animal. So we can get a very small margin of error for this specific recording/animal, but we cannot be as certain that this would generalize to other animals. But the interpretation of the results might depend a lot on what our assumptions are about inter-animal variability.
The measurement itself can be accurate and precise, despite imperfect instruments, indirect observations, and stochastic aspects to the process. That’s the similarity the post focuses on.
The individual-to-individual variability is a fascinating aspect to biology. I find Eve Marder’s work on this topic at the circuit level inspiring (e.g., https://doi.org/10.1016/j.conb.2014.10.012 ). I’ve been thinking a lot about it as a general principle for biology, not just neural circuitry— plasticity mechanisms to ensure conserved behavior despite variable components. I don’t have any insights to share at this point, but I’m enjoying working on it.
That said, some aspects of neural circuitry have very low individual-to-individual variability. For example, the layout of primary and higher visual areas in mouse cortex is pretty precise. See Supplementary Figure 1 in Riichiro’s recent manuscript (data for that figure is from coauthor Leah Townsend): https://doi.org/10.1101/2023.08.27.555017
Yes, I see your point.
And it’s always beautiful to see these almost-perfect registrations (in this supplementary figure 1) … I’ve never really worked on cortex proper, but this would be a reason to give it a try. Just today I watched an amazing lab meeting with super-precise mapping of 2P data to higher visual areas – always again impressive. With hippocampal imaging, I can only dream of that.