Measuring the gain of your imaging system
The images obtained from a 2-photon laser scanning microscope, or a CCD-based system, consist of an array of pixel values. For 8-bit images, each pixel value ranges from 0-255; for 16-bit images, the pixel values range from 0-65535. What do these numbers mean? Ideally, they’re linearly related to the number of photons detected for each pixel: pixel value = number of photons detected * g. The letter g stands for gain. It’s good to know this parameter. If the gain is less than 1, say 0.25, then 4 photons must be detected for an increase in pixel value of 1. If the gain is more than one, say 3, then each photon detected increases the pixel value by a magnitude of 3. As you can see, it’s good to have a gain higher than 1, so that each photon detected results in an increase in the pixel value; but gains above 1 are not typically necessary.
To measure the gain of an imaging system, we take advantage of the Poisson statistics of photon counting. Specifically, in a Poisson process like photon counting, which is effectively what all PMTs and CCDs do, the variance is equal to the mean.
Here is a general protocol that will work for PMT-based laser scanning microscopes (e.g., 2-photon LSM), and also CCD-based imaging systems (though there, the gain may be less than 1 and influenced by the electronics within the chip):
Step 1
Take a picture of some homogeneous object, a piece of fluorescent plastic works great (these slides from Ted Pella are a handy tool, but really any reasonably homogeneous source will work). Be sure to zoom in until there are no spatial inhomogeneities. If you need to, crop the image to the most homogeneous portion. Calculate the mean and standard deviation of the pixel values in that region. The gain of the system is (roughly) equal to the square of the standard deviation (aka the variance) divided by the mean. This is based on the fact that for a Poisson process, the variance is equal to the mean.
where g is the gain (in units of pixel values per photon), v is the pixel value, n is the number of photons, and m represents the mean of the subscripted variable. Similarly, for the standard deviation:
![]()
And the variance:
![]()
For a Poisson process, the variance is equal to the mean, so:
![]()
Rearrange the earlier equations to give:
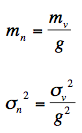
Substituting these two equations into the third one up from here and solving for g yields:

Step 2 (optional)
For a better gain measurement, turn the illumination intensity (e.g., laser power) up and down and repeat step 1 each time. Then plot the variance versus the mean and fit a linear regression. The slope is equal to the gain. In the plot above, we see how the voltage on the PMT affects the gain. The gain increases from 1.5 pixel values per photon at 0.5 volts, to 4.8 pixel values per photon at 0.6 volts.
Photons per pixel
Once you’ve computed the gain, you can compute the number of photons per pixel, on average. This is simply the mean pixel value divided by the gain. Of course, you can cut straight to the chase, skipping the gain calculation, by computing the square of the ratio of the mean pixel value to the standard deviation (start with the last three equations above if you want to derive it for yourself).
Final notes
The gain parameter we just computed is not a measure of sensitivity, it is a measure of how our digitally recorded signal relates to the actual photons detected. To measure sensitivity, we need to use a calibrated photon source and then measure the output based on the known source. For example, for PMTs we would calculate this as the PMT current per unit of incident light (amperes per watt). This can in turn be converted to quantum efficiency. See section 4.1.3 of Hamamatsu’s PMT Handbook for more details.
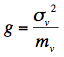

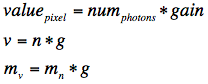

This is useful, but assumes that no additive offset has been applied. PMT offsets are often used to compensate for dark noise and preamp peculiarities, and most software programs can use a lookup table that doesn’t start at 0. This is a real problem when people want to calculate DF/F of course….
James Pawley commented on this analysis on the Confocal Listserv.
http://lists.umn.edu/cgi-bin/wa?A2=ind1502&L=confocalmicroscopy&P=1565
He enumerates a number of factors that can lead to errors in the above calculations. It’s a good read. Recommended.
He mentions multiplicative noise, which is also discussed a bit here:
http://labrigger.com/blog/2011/10/16/photon-counting-with-hybrid-pmts/
He also mentions DC offset, echoing dg’s comment above.
He also discusses filter and bandwidth considerations, which could be altered by the computer controlling the system without the operator knowing.
The ultimate message is: know what you’re measuring. Know how your imaging system works. It’s easy to misapply the above analysis. Make sure you’re measuring in a setting in which Poisson noise is the main noise source.
The link above, to Pawley’s comment in 2015, stopped working, so I pasted the whole thing here:
——————–
Hi all,
Thanks to Labrigger for working on this important topic.
However, I have read his analysis and think that the assumption that
one can use this procedure to measure the number of photoelectrons
(PE: i.e., detected photons) created at the photocathode (PC) of the
PMT may be an over-simplification.
The analysis depends on the assumption that the only source of noise
in the data recorded in the “image” of a flat white field is Poisson
Noise associated with the small number of PEs produced at the
photocathode. This might be true if PMTs were free from
multiplicative noise but in fact Poisson Noise also affects every
stage in the multiplication of a single PE after it leaves the PC. In
the very unusual case that the voltage between the PC and the first
dynode is 500-600 volts (and that this dynode has both the optimal
shape and the best GaAs surface), the gain of this stage may be 25
+/-5 or 20% additional noise. More commonly, this gain will be closer
to 4 +/-2 or 50% additional noise. More noise is added at each stage
and even though these noise terms are not additive (they are combined
as the sqrt of the sum of the squares), it is not at all uncommon for
this process to double or even triple the variation present in the
resulting signal beyond what one would expect from Poisson Noise
applied only to the number of PE. Furthermore, this added noise will
be somewhat larger if the system is working at a relatively high
signal level because then the PMT will be turned down, the gain/stage
correspondingly lower and the Poisson Noise proportionally higher.
Offsetting this error to some extent is the finite bandwidth of the
entire amplifier system (PMT plus the electronics between the final
dynode and the ADC). This bandwidth is in general unknown but may be
adjusted by the computer to more-or-less match what the computer
estimates is needed to pass the finest optical details that the
system can transmit on the basis of settings for wavelength,
objective NA, zoom/pixel size, and even PMT setting (high PMT voltage
implies a noisy signal that may benefit from the artificial,
1-dimensional smoothing that attends lower bandwidth).
Clearly, because bandwidth limits the maximum excursion that can be
transmitted between one pixel and its neighbour, it will tend to
reduce the apparent noise present in the digitized signal. The
magnitude of this clipping is unknown but may vary with the
parameters mentioned above.
This is relevant because, unlike the optical signal, the Poisson
Noise signal that we are searching for shows no correlation between
adjacent pixels. In particular, following the blog’s suggestion of
using a high zoom (to reduce fixed pattern noise) may cause the
computer to limit the bandwidth more than using a lower zoom.
Although, as noted above, because these two factors bias the results
in opposite directions, their effects may cancel each other out to
some extent. However, we need to know a lot more about how the
components are actually operating before we can decide whether and to
what extent this is true.
The analysis also assumes that there is no fixed patterns noise in
the image of a “flat white field” as might be caused, for instance,
by field curvature, spherical aberration, vignetting, dust or other
optical parameters that may change detected signal across the field
of view. I note that many of these sources of non-Poisson Noise can
be substantially reduced by recording two sequential frames and
obtaining a measure of the noise by subtracting one from the other.
For the analysis to work, it is also important to set the brightness
control (DC – offset) so that zero signal corresponds to closely to
zero intensity in the image memory.
I should note that multiplicative noise ceases to be a factor in
systems employing either hybrid PMT (where the first stage gain is
about 10,000) or effective photon-counting (i.e. a photon counting
where the recorded peak pixel signal is at least 10x smaller than the
saturation count rate of the system as set by pulse-pileup.).
One can avoid multiplcative noise by recording the data using a CCD
(but NOT on an EM-CCD used with the electronic gain turned on) and
the record-two-then-subtract approach can again be used to reduce
inevitable fixed pattern noise. However, this sensor will probably
work best when recording a fairly large signal (at least 10% of
peak?) so that read noise will be relatively insignificant. And as
above, the results will again be limited by the finite bandwidth of
the FET amplifier between the read-node and the ADC. Finally, when
using a CCD for quantitative measurements, it is particularly
important to remember that they are usually set up so that zero light
corresponds to 20-50 computer intensity units.
The noise performance of sCMOS detectors is both non-Gaussian and
depends strongly on the extent to which the internal pixel-by-pixel
variations in gain and offset are detected and corrected. This will
make their use for this type of measurement somewhat more difficult
unless the signal levels are well away from the noise floor.
Bottom line: Although the procedure may indeed give a useful
benchmark that we might call the “effective gain” of the signal path,
the measurement is subject to influence by a number of imaging
parameters and will not really allow one to measure how many
recorded-signal-intensity-units correspond to one PE.
Jim Pawley
[…] 2010, Labrigger wrote about how to measure the gain of a imaging system. As mentioned there in the comments, this was discussed in more detail by James Pawley in the […]
[…] recorded an image and determined the number of photons per pixel as described earlier (based on a Labrigger blog post). As far as I can tell from the small statistics for photon counting using oscilloscope […]