Z-Projections

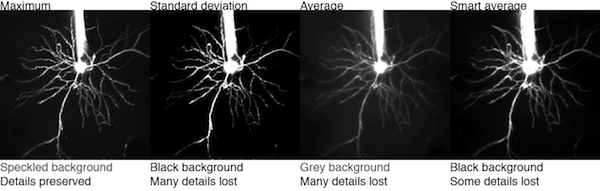
To project 3D image stacks to a 2D image, several different algortithms can be used. Maximum projections and averages are the most commonly used. Neither of these yield nice black backgrounds. In fact, maximum projections maximize the noise in the background. There are other options that do yield black backgrounds, including standard deviation projections and “smart” average projections (code and details below).

The best projection to use will depend on the source data and what type of information that needs to be conveyed. In this example, we’re looking at a layer 2/3 neuron in cortex with in vivo two photon imaging. The maximum projection looks very good, but if there was more noise in the background, then the smart average might have looked better.

What’s a smart average? It simply adds a thresholding step prior to averaging, so that slices with no signals do not contribute to the projection. Note that in this example, the background of the smart average is much blacker than the regular average projection. In this case, it still looks somewhat low-pass filtered compared to the maximum projection, though. Here’s the code:

macro Smart_Average{
	stackid=getImageID;
	no=nSlices;
	stackname=getTitle;
	run("Duplicate...", "title=[dup] duplicate range=1-no");
	setSlice((floor(no/2)));
	run("Threshold...");
	waitForUser("Set Threshold then click 'OK'.");
	setBatchMode(true);
	run("Convert to Mask", "  black");
	run("Divide...", "value=255 stack");
	rename("divided");
	bindupid=getImageID;
	imageCalculator("Multiply create stack", stackid ,bindupid);
	run("Z Project...", "start=1 stop=no projection=[Sum Slices]");
	rename(stackname+"sum");
	sumid=getImageID;
	setBatchMode(false);
	selectImage(bindupid);//closing and renaming actions must occur outside of the batch mode
	close();
}

From this listserv thread. Smart average code by G. MacDonald and K. Straatman.